题目信息

原题链接：https://leetcode.com/problems/smallest-subarrays-with-maximum-bitwise-or/

原题描述

给定一个长度为 n 的非负整数数组 nums，对于每一个索引 i，你需要找出从 i 开始的一个子数组（不能为空），使得该子数组中的元素按位或计算之后的结果是最大的，然后返回该数组的长度。也就是说对于任意的索引 i (0 <= i < n)，找到另一个索引 j (i <= j < n)，使得 Or[SubNums(i, j)] 最小，返回子数组长度即 j-i+1。

输入输出示例

Example 1

Input: nums = [1,0,2,1,3]
Output: [3,3,2,2,1]

Example 2

Input: nums = [1,2]
Output: [2,1]

条件约束

$ n == nums.length $
$ 1 \leqslant n \leqslant 10^5 $
$ 0 \leqslant nums[i] \leqslant 10^5 $

题解

分析

本题题意很好理解，让我们先从暴力解法开始逐步分析。

暴力解法是：对于每一个 i ，计算从 i 到 n-1 的每一个子数组的按位或值，找出值最大的子数组，取其长度即可。这种方法的时间复杂度为 $ O(n^2) $ ，考虑到原数组长度最大为 $ 10^5 $ ，这种方法肯定不可接受，最终会 TLE。

那么暴力解法是否还可以优化呢？比如是否可以通过某种方式记录子数组 SubNums(i, n-1) 的按位或值，然后逆向推到出来，这样对与每一个 i ，我们不需要重新计算所有的子数组了。这种方法对于加法操作是可以的，加法的话可以退化到使用“两指针法”求最大子数组长度了。本题的“或”运算不行，因为“或”没有逆运算。

让我们回到“或”运算上面来。我们知道，或运算是相同位上，只要有一个为 1 则结果为 1，两个都为 0 时结果才为 0 。那么要想让子数组或运算后的结果为最大，那么就是要让最终位运算值的每一位都尽可能是 1。

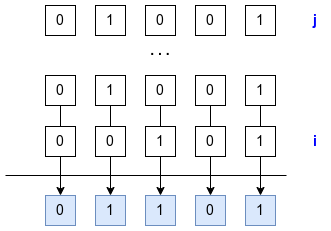
LeetCode-2441.drawio.png

如上图，对于第 i 个数，要想使他的某一位为 1，只需要从 i （包括 i 本身）开始往后找，找到第一个该位为 1 的数即可。那么如何确定 j 呢，只需要按照这个规则逐位查找，找到的最大的索引值即为 j。每次查找到的某位上为 1 的结果，可以存下来，这样就不用每次都重新计算了。需要特别注意，应尽可能每一位都查找，而不应该以当前 i 的最高位为准，因为在 i 后面可能存在更大的数。题目约束 $ nums[i] \leqslant 10^5 $ ，那么我们可以固定查找 $ log_2(10^5) \approx 16 $ 位，当然也可以在迭代过程中记录下当前最大的位数。

实现

我们可以定义一个 bitIndex 变量来记录每一位上值为 1 的最小的索引（确保子数组长度最短），然后逆向从 n-1 到 0 进行计算，对于 nums[i] 的第 k 位 nums[i]_k，如果 nums[i]_k 是 1，则不需要往后查找，同时更新 bitIndex[k] = i；如果 nums[i]_k 是 0，则需要与 bitIndex[k] 对应索引位置的数进行或运算才能使其为 1，此时 j = bitIndex[k]。按照这个方法找到的最大的 j 即为最终目标 j，子数组长度为 j-i+1。

最终实现的 Java 代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public int[] smallestSubarrays(int[] nums) {
    int[] res = new int[nums.length];
    int[] bitIndex = new int[32]; // 每一位上为 1 的数字的最小索引
    int highBit = 0; // 记录当前最高位
    Arrays.fill(bitIndex, -1);
    for (int i = nums.length-1; i >= 0; i--) {
        int nn = nums[i];
        int j = 0;
        int maxDis = 1;
        while (nn > 0 || j <= highBit) {
            highBit = Math.max(highBit, j);
            if (nn % 2 == 0) {
                if (bitIndex[j] > 0) {
                    maxDis = Math.max(maxDis, bitIndex[j]-i+1);
                }
            } else {
                bitIndex[j] = i;
            }
            nn >>= 1;
            j++;
        }
        res[i] = maxDis;
    }
    return res;
}

时间复杂度：$ O(n) $
空间复杂度：$ O(n) $