题目信息

原题链接：https://leetcode.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/

原题描述

假设有一段长度为 N 的木头，上面有若干个蚂蚁，每只蚂蚁都以相同的速度行走。蚂蚁每秒前进一个单位，当某只蚂蚁碰到另外一只蚂蚁时，就掉头朝一个方向行走（掉头没有时间损耗）。如果蚂蚁走到了木头的端点（0 或者 N），则蚂蚁会掉下木头。

现给定整数 n 表示木头的长度，给定整数数组 left 表示在 t0 时刻所有在朝左走的蚂蚁的位置，数组 right 表示在 t0 时刻所有朝右走的蚂蚁的位置，left 和 right 中没有重复元素。求所有蚂蚁都掉下木头所需的时间。

输入输出示例

• Example 1

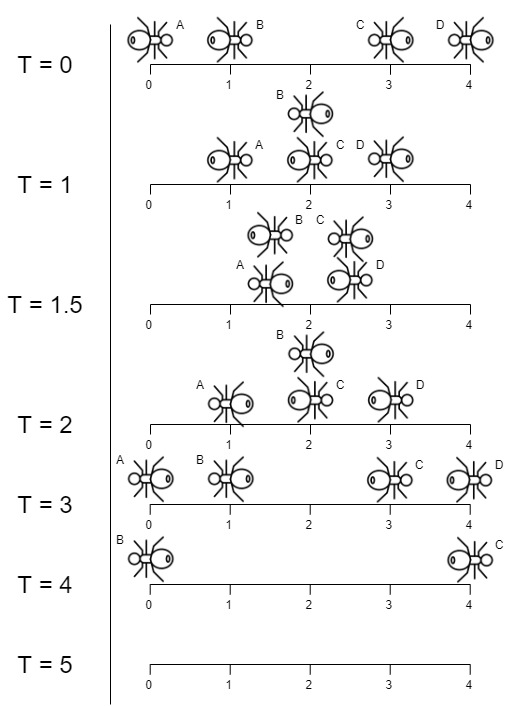
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
Explanation: 如图所示，我们把 4 只蚂蚁分别叫做 ABCD，在 t0 时刻，他们分别处在 0, 1, 3, 4 位置。
- 时间过去 1s 后（T=1），BC 在 2 位置相遇，各自掉头。此时 A 在 1 位置，D 在 3 位置，BD 朝左走，AC 朝右走。
- 时间过去 0.5s 后（T=1.5），AB 在 1.5 位置相遇，CD 在 2.5 位置相遇，各自掉头。此时，AB 朝左走，CD 朝右走。
- 时间过去 0.5s 后（T=2），BC 在 2 位置相遇，各自掉头。此时 A 在 1 位置，D 在 3 位置，AB 朝左走，CD 朝右走。
- 因为蚂蚁都朝着各自的一端走去，不会再相遇了，时间过去 1s 后（T=3），AD 到达断点位置，再过去 1s （T=4），BC 到达端点。
所以全部蚂蚁走到端点掉下木头需要 4s。

• Example 2

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: 由于所有蚂蚁都朝右走，当最后一次蚂蚁（即在位置 0 的蚂蚁）走到端点时，所有蚂蚁都掉下木头，即 7s。

条件约束

• $ 1 \leqslant n \leqslant 10^4 $
• $ 1 \leqslant left.length,right.lenght \leqslant n+1 $
• $ 1 \leqslant left[i],right[i] \leqslant n $
• $ 1 \leqslant left.lenght+right.length \leqslant n+1 $

题解

分析

本题看似很复杂，每只蚂蚁与另一只相遇的时间可以用递推公式算出来，而蚂蚁会不断的掉头，所以又像是要求极限，然而由于 left 和 right 大小可能不等，且分布的位置完全随即，出现的情况非常多，所以基本没法求极限计算。题目本身打了一个 Simulation 标签，那么是否可以通过模拟蚂蚁行为来求解呢？也不行，因为每一次移动需要重新计算所有蚂的位置，要求解 n 个蚂蚁最终的结果，那么需要进行 $ n*n $ 次计算，时间复杂度达到 $ O(n^2) $，结果肯定是 TLE。

让我们换一种思路，不要陷入题目设定的场景。

当两只蚂蚁相遇后，就会掉头继续行走，而所有蚂蚁的行走速度都是一样的，那么掉头的那个蚂蚁是不是相当于在替代另一只蚂蚁来走完它本来应该走的路呢？就拿例1来说，T=1 时，BC 相遇，B 掉头向左，C 掉头向右，此时如果我们把 BC 的标签换一下，这 4 只蚂蚁行走的场景是不变的。T=1.5 时，两对蚂蚁再次相遇，我们再次把相遇的蚂蚁的标签换一下，这 4 只蚂蚁行走的场景仍然是不变的。此时我们发现，换了标签之后，场景就变成了蚂蚁相遇后，不需要掉头，继续向前行走，那么我们只需要找到最后一只走下木头的蚂蚁就行了。

实现

要找到最后一只走下木头的蚂蚁，即找到 left 里面距离左端点最远的蚂蚁，right 里面距离右端点最远的蚂蚁。left 距离左端点的距离等于 left[i]，right 里面距离右端点的距离等于 n-right[i]，找到最大值即可。

最终实现的 Java 代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

public class Solution {
    public int getLastMoment(int n, int[] left, int[] right) {
        int max = 0;
        for (int pt : right) {
            max = Math.max(max, n - pt);
        }
        for (int pt : left) {
            max = Math.max(max, pt);
        }
        return max;
    }
}

• 时间复杂度：$ O(n) $
• 空间复杂度：$ O(1) $