题目信息

本题有两题，题干内容完全一致，只有约束条件在数量级上有差异。

原题链接：

1. https://leetcode.com/problems/count-beautiful-substrings-i
2. https://leetcode.com/problems/count-beautiful-substrings-ii

原题描述

给定一个字符串 s 和一个正整数 k，设 vowels 和 consonants 分别代表字符串中的元音字母数量和辅音字母数量。那么，如果一个字符串满足以下条件：

1. vowels == consonants
2. (vowels * consonants) % k == 0

则称该字符串为美丽字符串。

已知 s 中仅包含小写字母，求字符串 s 中所有的非空子美丽字符串 的数量。

输入输出示例

• Example 1

  Input: s = "baeyh", k = 2
  Output: 2
  Explanation: 子字符串 "baey" 和 "aeyh" 是目标美丽字符串，他们的元音和辅音字母数量都是 2 。
  

• Example 2

  Input: s = "abba", k = 1
  Output: 3
  Explanation: 子字符串 "ab" 和 "ba" 是目标美丽字符串，他们的元音和辅音字母数量都是 1 ；子字符串 "abba" 也是目标美丽子字符串，他们的元音和辅音字母数量都是 2 。
  

条件约束

• $ 1 \leqslant s.length \leqslant 1000 $  for MEDIUM, $ 1 \leqslant s.length \leqslant 50000 $  for HARD.
• $ 1 \leqslant k \leqslant 1000 $

题解 - MEDIUM

分析

美丽字符串的定义很好理解，即元音字母和辅音字母数量相等且他们的积是 k 的整数倍，题目要求找到所有的美丽子字符串。

对于求子字符串的题，首先可以考虑穷举法，对所有子字符串进行尝试，判断其是否满足条件。穷举法的时间复杂度是 $ O(n^2) $ ，考虑到本题中等难度下字符串长度最大为 1000，那么穷举法也是行的。

穷举法的每一次迭代，我们都需要检查对应的子字符串是否是美丽字符串，我们需要知道子字符串中的元音字母和辅音字母数量。如果每一次都重新统计的话，稍微有一点浪费。这里可以预先计算字母数量的前缀和 prefixSum，则每个字符串 sub(i,j) 中字母数量可以通过 prefixSum[j] - prefixSum[i-1] 得到。

关于美丽字符串的定义，还有 vowels == consonants 这个条件，这意味着字符串的长度一定是偶数，我们在穷举迭代中，可以将步长设置为 2 以减少迭代次数。

实现

定义长度与字符串 s 相等的前缀和数组 prefixSum，记录在每个位置上时元音字母的数量（只需要记录元音字母数量即可，辅音字母数量可以结合子字符串的长度计算出来。当然本题中元音数量和辅音数量完全相等，计算也可以省了）。

计算得到前缀和后，对以字符串的所有位置为起始位置的子字符串进行尝试，判断是否满足条件 2 即可。

最终实现的 Java 代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

public int beautifulSubstrings(String s, int k) {
    int[] prefixSum = new int[s.length()];
    for (int i = 0; i < s.length(); i++) {
        if (i > 0) {
            prefixSum[i] = prefixSum[i - 1];
        }
        char ch = s.charAt(i);
        if (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u') {
            prefixSum[i]++;
        }
    }

    int cnt = 0;
    for (int i = 0; i < s.length(); i++) {
        int pVowels = 0;
        if (i > 0) {
            pVowels = prefixSum[i - 1];
        }
        for (int j = i; j < s.length(); j += 2) {
            int vowels = prefixSum[j] - pVowels;
            int consonants = j - i + 1 - vowels;
            if (vowels == consonants && vowels * consonants % k == 0) {
                cnt++;
            }
        }
    }
    return cnt;
}

• 时间复杂度：$ O(n^2) $
• 空间复杂度：$ O(n) $

题解 - HARD

分析

MEDIUM 难度的数量级比较小，使用穷举法在时间复杂度上也是可以接受的。在 HARD 难度下，穷举法已经不适用了，即使结合 hash 进行优化，当 k=1 时，时间复杂度依然会退化到 O(n^2)，因此需要考虑其它方法。

不难得出，本题的数学问题是：给定 $ k $，找出所有的 $ x $ 使得 $ x^2 \pmod{k} = 0 $ 。假设子字符串长度为 $ L $，则 $ x = \frac{L}{2} $ ，则原等式转化为 $ (\frac{L}{2})^2 \pmod{k} = L^2 \pmod{4k} = 0 $。我们找出最小的长度 $ MIN(L) $，则在本题中，我们只需要检查所有长度为 $ x * MIN(L) $ 的子字符串即可，证明如下：

1. 设 L 为最小满足 $ L^2 \pmod{4k} = 0 $ 的值，则表明 $ L^2 = 4k $，即 $ L = 2\sqrt{k} $。用反证法。
2. 假设存在一个不是 $ L $ 的整数倍的数 $ xL + y $ 满足 $ (xL + y)^2 = 4k * n $，其中 $ x \geqslant 1, 1 < y < L, n > 1 $。
3. 将 $ (xL +y)^2 = 4k * n $ 两边开方并代入 $ L = 2\sqrt{k} $ 得到 $ x * 2\sqrt{k} + y = 2\sqrt{k} * \sqrt{n} $，移项并合并得到 $ y = 2\sqrt{k} * (\sqrt{n} - x) $。
4. 由于 $ y < L = 2\sqrt{k} $，则 $ 2\sqrt{k} * (\sqrt{n} - x) < 2\sqrt{k} $，也就是说 $ \sqrt{n} - x < 1 $ 必须成立，不难得出，唯一解为 $ n = x^2 $，此时 $ y = 0 $，与原始约束矛盾。

因此，要使 $ xL + y $ 满足条件，必须有 $ y = 0 $，我们只需要检测最小长度 $ L $ 的整数倍长度即可。

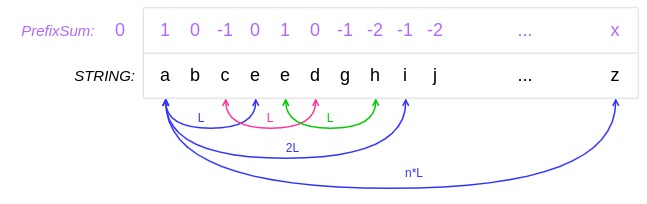
如上图，不难发现，有了最小长度 L，然后以 L 为区间找到所有最小的 L 长度的子字符串的位置，2L、3L、4L… nL 可以基于他们的拼接获取到。所有最小的 L 长度的子字符串为 sub(0, L-1), sub(L, 2L-1), ..., sub((n-1)L, nL-1)，sub(1, L), sub(L+1, 2L), ..., sub((n-1)L+1, nL), …, sub(L-1, 2L-2), sub(L, 3L-2), ...。

前面我们用了前缀和来简化子字符串中的元音字母和辅音字母的计算，结合上面的推论，我们只需要保证 $ prefixSum[j] - prefixSum[i-1] = xL $。用累加和的方式计算前缀和得到的结果是非递减的，要想利用前序计算结果需要重新做一次减法。

我们可以进一步优化。在计算前缀和的时候，不是采用累加的方式，而是遇到元音字母做 +1，遇到辅音字母做 -1，则当 $ prefixSum[j] = prefixSum[i-1] $ 的时候，sub(i, j) 子字符串中的元辅音字母数量一定相等，这样我们就可以用 Hash 表来记录前序计算结果了。需特别注意：字符串起始位置的前缀和为 0。

实现

首先计算最小长度 L。 然后可以通过一个 map 来记录 [0, L-1] 位置开始的以 L 为步长的，每一组子字符串的前缀和计算结果。 最后对每一组前缀和统计结果做求和运算即可。

最终实现的 Java 代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

public int beautifulSubstrings(String s, int k) {
    // get min L
    int L;
    for (L = 1; L * L % (4 * k) > 0; L++)
        ;
    // check all nL
    Map<Integer, Map<Integer, Integer>> map = new HashMap<>(L);
    for (int i = 0; i < L; i++) {
        Map<Integer, Integer> vMap = new HashMap<>();
        if (i == L - 1) { // at -1 position
            vMap.put(0, 1);
        }
        map.put(i, vMap);
    }
    int v = 0;
    for (int i = 0; i < s.length(); i++) {
        char ch = s.charAt(i);
        if (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u') {
            v += 1;
        } else {
            v -= 1;
        }
        // vMap record all value count
        Map<Integer, Integer> vMap = map.get(i % L);
        int c = vMap.getOrDefault(v, 0);
        vMap.put(v, c + 1);
    }
    int res = 0;
    for (Map<Integer, Integer> vMap : map.values()) {
        for (Integer c : vMap.values()) {
            res += (c - 1) * c / 2;
        }
    }
    return res;
}

• 时间复杂度：$ O(n + sqrt(k)) $
• 空间复杂度：$ O(n) $